PLUTO
Macros | Functions | Variables
quartic.devel1.c File Reference

Solve quartic and cubic equations-. More...

#include "pluto.h"
Include dependency graph for quartic.devel1.c:

Go to the source code of this file.

Macros

#define DEBUG   NO
 
#define swap(x, y)   f = x; x = y; y = f;
 
#define SWAP(x, y)   {double _t; _t = x; x = y; y = _t;}
 

Functions

void PrintSolution (double *z)
 
int QuarticNewton (double b, double c, double d, double e, double *z)
 
void QuarticPrintCoeffs (double b, double c, double d, double e)
 
double CheckSolution (double b, double c, double d, double e, double x)
 
double ResolventCubic (double b, double c, double d, double e, double x)
 
int QuarticSolveNew (double b, double c, double d, double e, double *z)
 
int QuadraticSolve (double a, double b, double c, double *x)
 
int QuarticSolve (double b, double c, double d, double e, double *z)
 
int CubicSolve (double b, double c, double d, double z[])
 

Variables

static int debug_print = DEBUG
 

Detailed Description

Solve quartic and cubic equations-.

Author
A. Mignone (migno.nosp@m.ne@p.nosp@m.h.uni.nosp@m.to.i.nosp@m.t)
Date
Sept 10, 2012

Definition in file quartic.devel1.c.

Macro Definition Documentation

#define DEBUG   NO

Definition at line 13 of file quartic.devel1.c.

#define swap (   x,
  y 
)    f = x; x = y; y = f;

Definition at line 30 of file quartic.devel1.c.

#define SWAP (   x,
  y 
)    {double _t; _t = x; x = y; y = _t;}

Definition at line 31 of file quartic.devel1.c.

Function Documentation

double CheckSolution ( double  b,
double  c,
double  d,
double  e,
double  x 
)

Definition at line 640 of file quartic.devel1.c.

644 {
645  double f, fp, fm, fmax;
646  f = e + x*(d + x*(c + x*(b + x)));
647 
648  x = 1.0;
649  fp = e + x*(d + x*(c + x*(b + x)));
650 
651  x = -1.0;
652  fm = e + x*(d + x*(c + x*(b + x)));
653 
654  fmax = MAX(fp,fm);
655  return f/fmax;
656 }
MAX
#define MAX(a, b)
Definition: macros.h:101
GRID::x
double * x
Definition: structs.h:80
menu.c
tuple c
Definition: menu.py:375
fp
FILE * fp
Definition: analysis.c:7

Here is the caller graph for this function:

int CubicSolve ( double  b,
double  c,
double  d,
double  z[] 
)

Solve a cubic equation in the form

\[ z^3 + bz^2 + cz + d = 0 \]

For its purpose, it is assumed that ALL roots are double. This makes things faster.

Parameters
[in]bcoefficient of the cubic
[in]ccoefficient of the cubic
[in]dcoefficient of the cubic
[out]zvector containing the roots of the cubic. Roots should be sorted in increasing order.

Reference: http://www.1728.com/cubic2.htm

Returns
Return 0 on success.

Definition at line 213 of file quartic.devel1.c.

233 {
234  double b2, g2;
235  double f, g, h;
236  double i, i2, j, k, m, n, p;
237  static double one_3 = 1.0/3.0, one_27=1.0/27.0;
238 
239  b2 = b*b;
240 
241 /* ----------------------------------------------
242  the expression for f should be
243  f = c - b*b/3.0; however, to avoid negative
244  round-off making h > 0.0 or g^2/4 - h < 0.0
245  we let c --> c(1- 1.1e-16)
246  ---------------------------------------------- */
247 
248  f = c*(1.0 - 1.e-16) - b2*one_3;
249  g = b*(2.0*b2 - 9.0*c)*one_27 + d;
250  g2 = g*g;
251  i2 = -f*f*f*one_27;
252  h = g2*0.25 - i2;
253 
254 /* --------------------------------------------
255  double roots are possible only when
256 
257  h <= 0
258  -------------------------------------------- */
259 
260  if (h > 1.e-12){
261 // printf ("Only one double root (%12.6e)!\n", h);
262  }
263  if (i2 < 0.0){
264 /*
265  printf ("i2 < 0.0 %12.6e\n",i2);
266  return(1);
267 */
268  i2 = 0.0;
269  }
270 
271 /* --------------------------------------
272  i^2 must be >= g2*0.25
273  -------------------------------------- */
274 
275  i = sqrt(i2); /* > 0 */
276  j = pow(i, one_3); /* > 0 */
277  k = -0.5*g/i;
278 
279 /* this is to prevent unpleseant situation
280  where both g and i are close to zero */
281 
282  k = (k < -1.0 ? -1.0:k);
283  k = (k > 1.0 ? 1.0:k);
284 
285  k = acos(k)*one_3; /* pi/3 < k < 0 */
286 
287  m = cos(k); /* > 0 */
288  n = sqrt(3.0)*sin(k); /* > 0 */
289  p = -b*one_3;
290 
291  z[0] = -j*(m + n) + p;
292  z[1] = -j*(m - n) + p;
293  z[2] = 2.0*j*m + p;
294 
295 /* ------------------------------------------------------
296  Since j, m, n > 0, it should follow that from
297 
298  z0 = -jm - jn + p
299  z1 = -jm + jn + p
300  z2 = 2jm + p
301 
302  z2 is the greatest of the roots, while z0 is the
303  smallest one.
304  ------------------------------------------------------ */
305 
306  return(0);
307 }
n
static int n
Definition: analysis.c:3
j
int j
Definition: analysis.c:2
k
int k
Definition: analysis.c:2
menu.c
tuple c
Definition: menu.py:375
i
int i
Definition: analysis.c:2

Here is the caller graph for this function:

void PrintSolution ( double *  z)

Definition at line 659 of file quartic.devel1.c.

663 {
664  print ("z = %f %f %f %f\n",z[0],z[1],z[2],z[3]);
665 }
print
void print(const char *fmt,...)
Definition: amrPluto.cpp:497

Here is the call graph for this function:

Here is the caller graph for this function:

int QuadraticSolve ( double  a,
double  b,
double  c,
double *  x 
)

Solve a quadratic equation in the form

ax^2 + bx + c = 0

Return roots in increasing order

Definition at line 679 of file quartic.devel1.c.

688 {
689  double del, sb, q;
690 
691  del = b*b - 4.0*a*c;
692  if (del < 0.0) return 1; /* No real root */
693 
694  if (b == 0){
695  x[1] = sqrt(c/a);
696  x[0] = -x[1];
697  }
698 
699  sb = (b > 0.0 ? 1.0:-1.0);
700  q = -0.5*(b + sb*sqrt(del));
701  x[0] = q/a;
702  x[1] = c/q;
703 
704  if (x[0] > x[1]) {
705  double scrh = x[1];
706  x[1] = x[0];
707  x[0] = scrh;
708  }
709 
710  return 0;
711 }
a
static double a
Definition: init.c:135
configure.scrh
tuple scrh
Definition: configure.py:200
GRID::x
double * x
Definition: structs.h:80
menu.c
tuple c
Definition: menu.py:375
q
static Runtime q
Definition: runtime_setup.c:490

Here is the caller graph for this function:

int QuarticNewton ( double  b,
double  c,
double  d,
double  e,
double *  z 
)

Solve the quartic equation using Newton method for multiple roots.

Reference

  • "A first course in Numerical Analysis" Ralston & Rabinowitz, Eq. [8.6-13] – [8.6-22]

Definition at line 571 of file quartic.devel1.c.

581 {
582  int k, max_iter=40;
583  double x, dx, f, df, d2f;
584  double tolx = 1.e-12, tolf = 1.e-18;
585 
586 
587  x = *z;
588  for (k = 0; k < max_iter; k++){
589  f = e + x*(d + x*(c + x*(b + x)));
590  df = d + x*(2.0*c + x*(3.0*b + 4.0*x));
591  d2f = 2.0*c + x*(6.0*b + 12.0*x);
592 
593  dx = f*df/(df*df - f*d2f); /* search for the root of u=f/df rather than f.
594  The increment than becomes
595  u/du = f*fd/(df^2 - f*d2f), see the
596  discussion before Eq. [8.6-22]. */
597  x -= dx;
598 
599  if (fabs(dx) < tolx || fabs(f) < tolf) {
600  *z = x;
601 
602 if (debug_print){
603  print ("QuarticNewton: k = %d, x = %f, dx = %12.6e, f = %8.3e\n",k,x, dx,f);
604  print ("QuarticNewton, root found in # %d iterations\n",k);
605 }
606  return 0;
607  }
608  }
609  print ("! QuarticNewton: too many steps\n");
610  return 1;
611 
612 }
debug_print
static int debug_print
Definition: quartic.devel1.c:24
GRID::dx
double * dx
Definition: structs.h:83
k
int k
Definition: analysis.c:2
print
void print(const char *fmt,...)
Definition: amrPluto.cpp:497
GRID::x
double * x
Definition: structs.h:80
menu.c
tuple c
Definition: menu.py:375

Here is the call graph for this function:

Here is the caller graph for this function:

void QuarticPrintCoeffs ( double  b,
double  c,
double  d,
double  e 
)

Definition at line 616 of file quartic.devel1.c.

620 {
621  print ("! f(x) = %18.12e + x*(%18.12e + x*(%18.12e ",
622  e, d, c);
623  print (" + x*(%18.12e + x*%18.12e)))\n", b, 1.0);
624 
625  print ("b = %18.14e;\n",b);
626  print ("c = %18.14e;\n",c);
627  print ("d = %18.14e;\n",d);
628  print ("e = %18.14e;\n",e);
629 
630  double b3 = -2.0*c;
631  double c3 = c*c + b*d - 4.0*e;
632  double d3 = -(b*c*d - b*b*e - d*d);
633 
634  print ("! Resolvent cubic:\n");
635  print ("! g(x) = %18.12e + x*(%18.12e + x*(%18.12e + x))\n", d3, c3, b3);
636 
637 }
print
void print(const char *fmt,...)
Definition: amrPluto.cpp:497
menu.c
tuple c
Definition: menu.py:375

Here is the call graph for this function:

Here is the caller graph for this function:

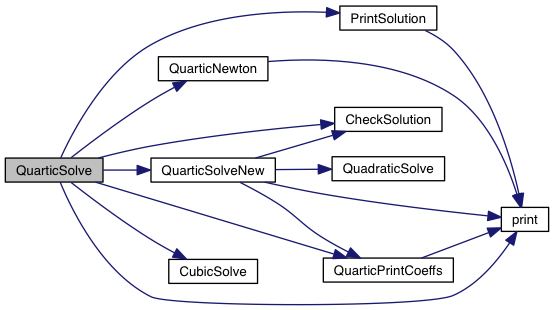
int QuarticSolve ( double  b,
double  c,
double  d,
double  e,
double *  z 
)

Solve a quartic equation in the form

\[ z^4 + bz^3 + cz^2 + dz + e = 0 \]

For its purpose, it is assumed that ALL roots are double. This makes things faster.

Parameters
[in]bcoefficient of the quartic
[in]ccoefficient of the quartic
[in]dcoefficient of the quartic
[in]ecoefficient of the quartic
[out]zvector containing the (double) roots of the quartic

Reference:

http://www.1728.com/quartic2.htm

Returns
Return 0 on success, 1 if cubic solver fails, 2 if NaN has been found and 3 if quartic is not satisfied.

Definition at line 34 of file quartic.devel1.c.

58 {
59  int n, j, ifail;
60  double b2, f, g, h;
61  double a2, a1, a0, u[4];
62  double p, q, r, s;
63  static double three_256 = 3.0/256.0;
64  static double one_64 = 1.0/64.0;
65 
66 #if DEBUG == YES
67 QuarticSolveNew(b,c,d,e,z);
68 PrintSolution(z);
69 exit(1);
70 #endif
71 
72  b2 = b*b;
73 
74  f = c - b2*0.375;
75  g = d + b2*b*0.125 - b*c*0.5;
76  h = e - b2*b2*three_256 + 0.0625*b2*c - 0.25*b*d;
77 
78  a2 = 0.5*f;
79  a1 = (f*f - 4.0*h)*0.0625;
80  a0 = -g*g*one_64;
81 
82  ifail = CubicSolve(a2, a1, a0, u);
83 
84  if (ifail) return 1;
85 
86  if (u[1] < 1.e-14){
87 
88  p = sqrt(u[2]);
89  s = 0.25*b;
90  z[0] = z[2] = - p - s;
91  z[1] = z[3] = + p - s;
92 
93  }else{
94 
95  p = sqrt(u[1]);
96  q = sqrt(u[2]);
97 
98  r = -0.125*g/(p*q);
99  s = 0.25*b;
100 
101  z[0] = - p - q + r - s;
102  z[1] = p - q - r - s;
103  z[2] = - p + q - r - s;
104  z[3] = p + q + r - s;
105 
106  }
107 
108 /* ----------------------------------------
109  Sort roots in ascending order.
110  Since z[0] < z[3], we first order
111 
112  z[0] < z[1] < z[3]
113 
114  and then put z[2] into the sequence.
115  ---------------------------------------- */
116 
117  if (z[1] < z[0]) {swap(z[1],z[0]);}
118  else if (z[1] > z[3]) {swap(z[1],z[3]);}
119 
120 
121  if (z[2] < z[0]) {
122  swap(z[2],z[0]);
123  swap(z[2],z[1]);
124  }else if (z[2] < z[1]){
125  swap(z[2],z[1]);
126  }else if (z[2] > z[3]){
127  swap(z[2],z[3]);
128  }
129 
130 /*
131  for (j = 1; j < 4; j++){
132  f = z[j];
133  n = j - 1;
134  while(n >= 0 && z[n] > f) {
135  z[n+1] = z[n];
136  n--;
137  }
138  z[n+1] = f;
139  }
140 */
141 
142  /* ----------------------------------------------
143  verify that cmax and cmin satisfy original
144  equation
145  ---------------------------------------------- */
146 
147  for (n = 0; n < 4; n++){
148  s = e + z[n]*(d + z[n]*(c + z[n]*(b + z[n])));
149  if (s != s) {
150 // print ("! QuarticSolve: NaN found.\n");
151  return 2;
152  }
153  if (fabs(s) > 1.e-6) {
154 // print ("! QuarticSolve: solution does not satisfy f(z) = 0; f(z) = %12.6e\n",s);
155  return 3;
156  }
157  }
158 
159 
160  double znew[4];
161  ifail = QuarticSolveNew(b,c,d,e,znew);
162  if (ifail) {
163  debug_print = 1;
164  ifail = QuarticSolveNew(b,c,d,e,znew);
165  print ("QuarticSolveNew() has failed\n");
166  QUIT_PLUTO(1);
167  }
168  for (n = 0; n < 4; n++){
169  if (znew[n] != znew[n]) {
170  print ("! QuarticSolve(): nan in root %d\n",n);
171  debug_print = 1;
172  ifail = QuarticSolveNew(b,c,d,e,znew);
173  QUIT_PLUTO(1);
174  }
175  }
176 
177 
178  if (fabs(z[0]-znew[0]) > 1.e-3 || fabs(z[3]-znew[3]) > 1.e-3){
179  debug_print = 1;
180  QuarticSolveNew(b,c,d,e,znew);
181 
182  printf ("! Different solutions\n");
183  print (" Old: "); PrintSolution(z);
184  print (" Verify[0]: %12.6e\n",CheckSolution(b,c,d,e,z[0]));
185  print (" Verify[3]: %12.6e\n",CheckSolution(b,c,d,e,z[3]));
186 
187  print ("\n");
188  print (" New: "); PrintSolution(znew);
189  print (" Verify[0]: %12.6e\n",CheckSolution(b,c,d,e,znew[0]));
190  print (" Verify[3]: %12.6e\n",CheckSolution(b,c,d,e,znew[3]));
191  print ("\n Now improving with Newton\n");
192 
193 
194  QuarticNewton(b,c,d,e,znew);
195  QuarticNewton(b,c,d,e,znew+3);
196  print (" Improved:"); PrintSolution(znew);
197  print (" Verify[0]: %12.6e\n",CheckSolution(b,c,d,e,znew[0]));
198  print (" Verify[3]: %12.6e\n",CheckSolution(b,c,d,e,znew[3]));
199 
200  QuarticPrintCoeffs(b,c,d,e);
201  QUIT_PLUTO(1);
202  }
203  z[0] = znew[0];
204  z[3] = znew[3];
205 
206  return(0);
207 /*
208  printf (" z: %f ; %f ; %f ; %f\n",z[0], z[1], z[2], z[3]);
209  */
210 }
n
static int n
Definition: analysis.c:3
CubicSolve
int CubicSolve(double b, double c, double d, double z[])
Definition: quartic.devel1.c:213
debug_print
static int debug_print
Definition: quartic.devel1.c:24
QuarticNewton
int QuarticNewton(double b, double c, double d, double e, double *z)
Definition: quartic.devel1.c:571
CheckSolution
double CheckSolution(double b, double c, double d, double e, double x)
Definition: quartic.devel1.c:640
PrintSolution
void PrintSolution(double *z)
Definition: quartic.devel1.c:659
j
int j
Definition: analysis.c:2
print
void print(const char *fmt,...)
Definition: amrPluto.cpp:497
QuarticSolveNew
int QuarticSolveNew(double b, double c, double d, double e, double *z)
Definition: quartic.devel1.c:319
menu.c
tuple c
Definition: menu.py:375
s
#define s
swap
#define swap(x, y)
Definition: quartic.devel1.c:30
q
static Runtime q
Definition: runtime_setup.c:490
QUIT_PLUTO
#define QUIT_PLUTO(e_code)
Definition: macros.h:125
QuarticPrintCoeffs
void QuarticPrintCoeffs(double b, double c, double d, double e)
Definition: quartic.devel1.c:616

Here is the call graph for this function:

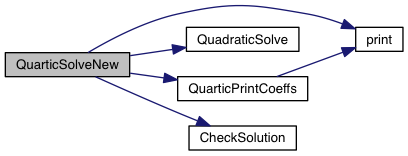
int QuarticSolveNew ( double  b,
double  c,
double  d,
double  e,
double *  z 
)

Solve a quartic equation in the form

\[ z^4 + bz^3 + cz^2 + dz + e = 0 \]

For its purpose, it is assumed that ALL roots are double. This makes things faster.

Parameters
[in]bcoefficient of the quartic
[in]ccoefficient of the quartic
[in]dcoefficient of the quartic
[in]ecoefficient of the quartic
[out]zvector containing the (double) roots of the quartic

Reference:

https://en.wikipedia.org/wiki/Quartic_function

Returns
Return 0 on success.

Definition at line 319 of file quartic.devel1.c.

343 {
344  int status, k;
345  double scrh, p, q, del, del0, del1, Q, S, Y;
346  double sqp, sqm, phi, sq_del0;
347  double D, P;
348  double den, bnorm, dnorm;
349  double zmin, zmax;
350  const double one_third = 1.0/3.0;
351 
352 #if DEBUG == YES
353 /* -- four distinct roots in 3/10, -9/10, 9/10, 5/10 -- */
354 /*
355 b = -4.0/5.0;
356 c = -33.0/50.0;
357 d = 81.0/125.;
358 e = -243./2.e3;
359 */
360 /* -- Two simple roots (6/10, -75/100) and one double root (2/10) -- */
361 /*
362 b = -0.25;
363 c = -0.47;
364 d = 93.0/500.0;
365 e = -9.0/500.;
366 */
367 /* -- two double roots, 9/10 and -7/10 -- */
368 /*
369 e = 3969/1.e4;
370 d = 63./250.0;
371 c = -61./50.0;
372 b = -2.0/5.0;
373 */
374 
375 /* -- One quadrupole root in 0.99 -- */
376 /*
377 b = - 99./25.0;
378 c = 29403./5000.;
379 d = -970299./250.e3;
380 e = 96059601./1.e8;
381 */
382 
383 /* -- Four distinct roots, very close -- */
384 
385 b = -3.97367591434748e+00;
386 c = 5.92126911218894e+00;
387 d = -3.92150958389634e+00;
388 e = 9.73916387216783e-01;
389 
390 /*
391 QuarticNewton (b,c,d,e,z);
392 print ("\n\n\n Using Newton:\n");
393 printf ("min and max roots = %12.6e, %12.6e\n",z[0],z[3]);
394 exit(1);
395 */
396 #endif
397 
398  double b2 = b*b, c2=c*c, bd=b*d;
399 
400  del0 = c2 - 3.0*bd + 12.0*e; /* scales as a^2 */
401  del1 = c*(2.0*c2 - 9.0*bd) + 27.0*(b2*e + d*d) - 72.0*c*e; /* scales as a^3 */
402  del = (4.0*del0*del0*del0 - del1*del1)/27.0; /* >= 0.0, scales as a^6 */
403  D = 64.0*e - 16.0*c2 + 16.0*b2*c - 16.0*bd - 3.0*b2*b2; /* scales as a^4 */
404  P = 8.0*c - 3.0*b2;
405 
406  Y = 0.25*b2 + 2.0*d/(b+1.e-40) - c;
407 
408  den = 1.0 + fabs(b) + fabs(c) + fabs(d);
409  bnorm = fabs(b)/den;
410  dnorm = fabs(d)/den;
411 
412 //#if DEBUG == YES
413  if (debug_print){
414  print ("QuarticSolve(): del = %12.6e, del0 = %12.6e D = %12.6e, P = %12.6e, Y = %12.6e\n",
415  del,del0, D,P, Y);
416  }
417 /*
418  4 distinct roots: del > 0
419  2 simple, 1 double: del = 0, P < 0, D < 0, del0 != 0
420  2 double: del = 0, P < 0, D = 0
421  1 triple: del = 0, D != 0
422  1 quadrupole: del = 0, del0 = 0, D = 0
423 
424 */
425 //#endif
426 
427 
428 double zero = 1.e-12;
429 double zero2 = zero*zero;
430 double zero3 = zero2*zero;
431 
432 
433  if (fabs(del) < zero3 && fabs(del0) < zero && fabs(D) < zero2){
434 if (debug_print) print ("Case A: QuarticSolve(): 1 quadrupole root\n");
435  z[0] = z[1] = z[2] = z[3] = -0.25*b;
436  } else if (bnorm < 1.e-12 && dnorm < 1.e-12){ /* Bi-quadratic */
437 if (debug_print) print ("Case B: QuarticSolve(): Biquadratic\n");
438  double a2 = 1.0, b2 = c, c2 = e;
439  double x[2];
440  QuadraticSolve (a2,b2,c2,x);
441 
442  x[0] = MAX(0.0, x[0]);
443  x[1] = MAX(0.0, x[1]);
444 
445  if (x[0] < 0.0 || x[1] < 0.0){
446  print ("QuarticSolve(): case B: cannot continue\n");
447  print ("x = %12.6e, %12.6e\n",x[0],x[1]);
448  QUIT_PLUTO(1);
449  }
450  z[0] = -sqrt(x[1]);
451  z[1] = -sqrt(x[0]);
452  z[2] = sqrt(x[0]);
453  z[3] = sqrt(x[1]);
454 
455  } else if (fabs(Y) < 1.e-14){
456 if (debug_print) print ("Case C: QuarticSolve(): No need for resolvent cubic\n");
457  double x[2];
458  double a2, b2, c2, del2;
459 
460  a2 = 1.0;
461  b2 = 0.5*b;
462  del2 = d*d/(b*b) - e;
463  del2 = MAX(0.0, del2); /* Prevent small roundoff */
464  if (del2 < 0.0){
465  print ("! QuarticSolve(): case C: cannot continue, del2 = %12.6e\n",del2);
466  QuarticPrintCoeffs(b,c,d,e);
467  QUIT_PLUTO(1);
468  }
469  c2 = d/b + sqrt(del2);
470  status = QuadraticSolve(a2,b2,c2,x);
471  z[0] = x[0];
472  z[3] = x[1];
473 
474  c2 = d/b - sqrt(del2);
475  status = QuadraticSolve(a2,b2,c2,x);
476  z[1] = x[0];
477  z[2] = x[1];
478 
479  } else { /* Non degenerate case. Implies del0 > 0 */
480 
481 if (debug_print) {
482  print ("- QuarticSolve(): case 4: 4 distinct roots, no degeneracy\n");
483  print (" del0 = %12.6e, del1 = %12.6e\n",del0, del1);
484 }
485 
486 del0 = MAX(del0,0.0);
487  sq_del0 = sqrt(del0);
488  scrh = 0.5*del1/(fabs(del0)*sq_del0); /* This is always less than 1
489  (in fabs) since del > 0 */
490 if (debug_print) print (" scrh = %8.3e\n",scrh);
491 scrh = MAX(scrh,-1.0);
492 scrh = MIN(scrh, 1.0);
493  phi = acos(scrh)*one_third;
494  p = c - 3.0*b*b/8.0;
495  q = 0.125*b*b*b - 0.5*b*c + d; /* this is bY/2 */
496 
497  scrh = -2.0*(p - sq_del0*cos(phi))*one_third;
498 
499 scrh = MAX(scrh,0.0);
500  if (scrh < 0.0){
501  print ("! Quartic(): canont compute S, scrh = %12.6e\n",scrh);
502  return 1;
503  }
504 
505 
506  S = 0.5*sqrt(scrh); /* > 0 */
507 if (debug_print) print (" S = %12.6e\n",S);
508  if (fabs(S) < 1.e-12){
509  print ("! Quartic(): S = %12.6e <= 0 \n",S);
510  return 2;
511  }
512 
513  scrh = -4.0*S*S - 2.0*p - q/S;
514  scrh = MAX(0.0, scrh);
515 if (debug_print) print (" sqp^2 = %12.6e\n",scrh);
516  sqm = sqrt(scrh);
517  scrh = -4.0*S*S - 2.0*p + q/S;
518  scrh = MAX(0.0, scrh);
519 if (debug_print) print (" sqp^2 = %12.6e\n",scrh);
520  sqp = sqrt(scrh);
521 
522  /* -- Sort roots by increasing value.
523  This ordering has been established on testing only. -- */
524 
525  z[0] = -0.25*b - S - 0.5*sqp;
526  z[1] = -0.25*b - S + 0.5*sqp;
527  z[2] = -0.25*b + S - 0.5*sqm;
528  z[3] = -0.25*b + S + 0.5*sqm;
529 
530 
531 if (fabs(CheckSolution(b,c,d,e,z[0]))>1.e-8){
532  print ("! QuarticSolve: not correct (0)\n");
533  QUIT_PLUTO(1);
534 }
535 
536  }
537 
538 /* --------------------------------------------------------
539  Check and sort
540  -------------------------------------------------------- */
541 
542 
543 /*
544 if (! ( (z[0] <= z[1]) && (z[1] <= z[2]) && (z[2] <= z[3]))){
545  print ("! QuarticSolve: roots are not correctly ordered\n");
546  print ("! S = %12.6e, sqp = %12.6e, sqm = %12.6e\n",S,sqp,sqm);
547  PrintSolution(z);
548  QUIT_PLUTO(1);
549 }
550 */
551 
552 /* Sort roots in ascending order */
553 /*
554  if (z[1] < z[0]) {SWAP(z[1],z[0]);}
555  else if (z[1] > z[3]) {SWAP(z[1],z[3]);}
556 
557 
558  if (z[2] < z[0]) {
559  SWAP(z[2],z[0]);
560  SWAP(z[2],z[1]);
561  }else if (z[2] < z[1]){
562  SWAP(z[2],z[1]);
563  }else if (z[2] > z[3]){
564  SWAP(z[2],z[3]);
565  }
566 */
567  return 0;
568 }
MAX
#define MAX(a, b)
Definition: macros.h:101
debug_print
static int debug_print
Definition: quartic.devel1.c:24
configure.scrh
tuple scrh
Definition: configure.py:200
flow_past_cyc.D
tuple D
Definition: flow_past_cyc.py:11
Y
#define Y
Definition: radiat.modified_by_Bhargav.c:4
MIN
#define MIN(a, b)
Definition: macros.h:104
CheckSolution
double CheckSolution(double b, double c, double d, double e, double x)
Definition: quartic.devel1.c:640
k
int k
Definition: analysis.c:2
print
void print(const char *fmt,...)
Definition: amrPluto.cpp:497
GRID::x
double * x
Definition: structs.h:80
menu.c
tuple c
Definition: menu.py:375
QuadraticSolve
int QuadraticSolve(double a, double b, double c, double *x)
Definition: quartic.devel1.c:679
q
static Runtime q
Definition: runtime_setup.c:490
QUIT_PLUTO
#define QUIT_PLUTO(e_code)
Definition: macros.h:125
QuarticPrintCoeffs
void QuarticPrintCoeffs(double b, double c, double d, double e)
Definition: quartic.devel1.c:616

Here is the call graph for this function:

Here is the caller graph for this function:

double ResolventCubic ( double  b,
double  c,
double  d,
double  e,
double  x 
)

Definition at line 667 of file quartic.devel1.c.

668 {
669  double b3,c3,d3, f;
670 
671  b3 = -2.0*c;
672  c3 = c*c + b*d - 4.0*e;
673  d3 = -(b*c*d - b*b*e - d*d);
674  f = d3 + x*(c3 + x*(b3 + x));
675  return f;
676 }
GRID::x
double * x
Definition: structs.h:80
menu.c
tuple c
Definition: menu.py:375

Variable Documentation

int debug_print = DEBUG
static

Definition at line 24 of file quartic.devel1.c.