PLUTO
Functions
init.c File Reference

Two-dimensional Riemann problem. More...

#include "pluto.h"
Include dependency graph for init.c:

Go to the source code of this file.

Functions

void Init (double *us, double x1, double x2, double x3)
 
void Analysis (const Data *d, Grid *grid)
 
void UserDefBoundary (const Data *d, RBox *box, int side, Grid *grid)
 

Detailed Description

Two-dimensional Riemann problem.

Sets the initial condition for the 2D Riemann problem described in Mignone et al. (2005). The computational domain is initially divided into four states and the outcoming wave pattern involves the formtation of 2 shocks and two contact waves.

rhd_riemann2D.01.jpg
Final state for configuration #01.
Authors
A. Mignone (migno.nosp@m.ne@p.nosp@m.h.uni.nosp@m.to.i.nosp@m.t)
Date
July 09, 2014

Reference:

  • "The Piecewise Parabolic Method for Multidimensional Relativistic Fluid Dynamics", Mignone, Plewa & Bodo, ApJS (2005)

Definition in file init.c.

Function Documentation

void Analysis ( const Data *  d,
Grid *  grid 
)

Perform runtime data analysis.

Parameters
[in]dthe PLUTO Data structure
[in]gridpointer to array of Grid structures

Compute volume-integrated magnetic pressure, Maxwell and Reynolds stresses. Save them to "averages.dat"

Definition at line 68 of file init.c.

73 {
74 
75 }
void Init ( double *  us,
double  x1,
double  x2,
double  x3 
)

The Init() function can be used to assign initial conditions as as a function of spatial position.

Parameters
[out]va pointer to a vector of primitive variables
[in]x1coordinate point in the 1st dimension
[in]x2coordinate point in the 2nd dimension
[in]x3coordinate point in the 3rdt dimension

The meaning of x1, x2 and x3 depends on the geometry:

\[ \begin{array}{cccl} x_1 & x_2 & x_3 & \mathrm{Geometry} \\ \noalign{\medskip} \hline x & y & z & \mathrm{Cartesian} \\ \noalign{\medskip} R & z & - & \mathrm{cylindrical} \\ \noalign{\medskip} R & \phi & z & \mathrm{polar} \\ \noalign{\medskip} r & \theta & \phi & \mathrm{spherical} \end{array} \]

Variable names are accessed by means of an index v[nv], where nv = RHO is density, nv = PRS is pressure, nv = (VX1, VX2, VX3) are the three components of velocity, and so forth.

Definition at line 25 of file init.c.

31 {
32  double x, y, scrh;
33 
34  x = x1;
35  y = x2;
36 
37  us[VX1] = us[VX2] = 0.0;
38  if (x > 0.0 && y > 0.0){
39  us[RHO] = 5.477875e-3;
40  us[PRS] = 2.762987e-3;
41  us[VX1] = 0.0;
42  us[VX2] = 0.0;
43  }else if(x < 0.0 && y > 0.0){
44  us[RHO] = 0.1;
45  us[PRS] = 1.0;
46  us[VX1] = 0.99;
47  us[VX2] = 0.0;
48  }else if(x < 0.0 && y < 0.0){
49  us[RHO] = 0.5;
50  us[PRS] = 1.0;
51  us[VX1] = 0.0;
52  us[VX2] = 0.0;
53  }else if(x > 0.0 && y < 0.0){
54  us[RHO] = 0.1;
55  us[PRS] = 1.0;
56  us[VX1] = 0.0;
57  us[VX2] = 0.99;
58  }
59 
60  #if USE_FOUR_VELOCITY == YES
61  scrh = 1.0/sqrt(1.0 - us[VX1]*us[VX1] - us[VX2]*us[VX2]);
62  us[VX1] *= scrh;
63  us[VX2] *= scrh;
64  #endif
65 
66 }
VX2
#define VX2
Definition: mod_defs.h:29
RHO
#define RHO
Definition: mod_defs.h:19
configure.scrh
tuple scrh
Definition: configure.py:200
VX1
#define VX1
Definition: mod_defs.h:28
GRID::x
double * x
Definition: structs.h:80
void UserDefBoundary ( const Data *  d,
RBox *  box,
int  side,
Grid *  grid 
)

Assign user-defined boundary conditions.

Parameters
[in,out]dpointer to the PLUTO data structure containing cell-centered primitive quantities (d->Vc) and staggered magnetic fields (d->Vs, when used) to be filled.
[in]boxpointer to a RBox structure containing the lower and upper indices of the ghost zone-centers/nodes or edges at which data values should be assigned.
[in]sidespecifies the boundary side where ghost zones need to be filled. It can assume the following pre-definite values: X1_BEG, X1_END, X2_BEG, X2_END, X3_BEG, X3_END. The special value side == 0 is used to control a region inside the computational domain.
[in]gridpointer to an array of Grid structures.

Assign user-defined boundary conditions in the lower boundary ghost zones. The profile is top-hat:

\[ V_{ij} = \left\{\begin{array}{ll} V_{\rm jet} & \quad\mathrm{for}\quad r_i < 1 \\ \noalign{\medskip} \mathrm{Reflect}(V) & \quad\mathrm{otherwise} \end{array}\right. \]

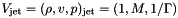where $ V_{\rm jet} = (\rho,v,p)_{\rm jet} = (1,M,1/\Gamma)$ and M is the flow Mach number (the unit velocity is the jet sound speed, so 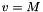$ v = M$).

Assign user-defined boundary conditions:

  • left side (x beg): constant shocked values
  • bottom side (y beg): constant shocked values for x < 1/6 and reflective boundary otherwise.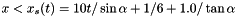
  • top side (y end): time-dependent boundary: for $ x < x_s(t) = 10 t/\sin\alpha + 1/6 + 1.0/\tan\alpha $ we use fixed (post-shock) values. Unperturbed values otherwise.

Assign user-defined boundary conditions at inner and outer radial boundaries. Reflective conditions are applied except for the azimuthal velocity which is fixed.

Assign user-defined boundary conditions.

Parameters
[in/out]d pointer to the PLUTO data structure containing cell-centered primitive quantities (d->Vc) and staggered magnetic fields (d->Vs, when used) to be filled.
[in]boxpointer to a RBox structure containing the lower and upper indices of the ghost zone-centers/nodes or edges at which data values should be assigned.
[in]sidespecifies on which side boundary conditions need to be assigned. side can assume the following pre-definite values: X1_BEG, X1_END, X2_BEG, X2_END, X3_BEG, X3_END. The special value side == 0 is used to control a region inside the computational domain.
[in]gridpointer to an array of Grid structures.

Set the injection boundary condition at the lower z-boundary (X2-beg must be set to userdef in pluto.ini). For 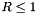$ R \le 1 $ we set constant input values (given by the GetJetValues() function while for $ R > 1 $ the solution has equatorial symmetry with respect to the z=0 plane. To avoid numerical problems with a "top-hat" discontinuous jump, we smoothly merge the inlet and reflected value using a profile function Profile().

Provide inner radial boundary condition in polar geometry. Zero gradient is prescribed on density, pressure and magnetic field. For the velocity, zero gradient is imposed on v/r (v = vr, vphi).

The user-defined boundary is used to impose stress-free boundary and purely vertical magnetic field at the top and bottom boundaries, as done in Bodo et al. (2012). In addition, constant temperature and hydrostatic balance are imposed. For instance, at the bottom boundary, one has:

\[ \left\{\begin{array}{lcl} \DS \frac{dp}{dz} &=& \rho g_z \\ \noalign{\medskip} p &=& \rho c_s^2 \end{array}\right. \qquad\Longrightarrow\qquad \frac{p_{k+1}-p_k}{\Delta z} = \frac{p_{k} + p_{k+1}}{2c_s^2}g_z \]

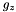where $g_z$ is the value of gravity at the lower boundary. Solving for 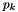$p_k$ at the bottom boundary where 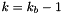$k=k_b-1$ gives:

\[ \left\{\begin{array}{lcl} p_k &=& \DS p_{k+1} \frac{1-a}{1+a} \\ \noalign{\medskip} \rho_k &=& \DS \frac{p_k}{c_s^2} \end{array}\right. \qquad\mathrm{where}\qquad a = \frac{\Delta z g_z}{2c_s^2} > 0 \]

where, for simplicity, we keep constant temperature in the ghost zones rather than at the boundary interface (this seems to give a more stable behavior and avoids negative densities). A similar treatment holds at the top boundary.

Assign user-defined boundary conditions. At the inner boundary we use outflow conditions, except for velocity which we reset to zero when there's an inflow

Definition at line 77 of file init.c.

82 { }