|
PLUTO
|
Propagation of a conduction front. More...
#include "pluto.h"
Go to the source code of this file.
Functions | |
| void | Init (double *us, double x1, double x2, double x3) |
| void | Analysis (const Data *d, Grid *grid) |
| void | UserDefBoundary (const Data *d, RBox *box, int side, Grid *grid) |
Propagation of a conduction front.
The problem sets the initial condition for a propagating conduction front for which an analytical solution exists (Reale 1995).
The equation
![\[ \frac{\partial T}{\partial t} = a\frac{\partial}{\partial s} \left(T^n\frac{\partial T}{\partial s}\right) \]](form_406.png)
has the solution
![\[ T = T_c\left(1 - \frac{s^2}{s_f^2}\right)^{1/n} \]](form_407.png)
where
![\[ T_c = \left(\frac{Q^2}{at}\right)^{1/(n+2)} \left(\frac{n}{2(n+2)}\zeta_0^2\right)^{1/n}\,, \quad\quad\quad s_f = (aQ^nt)^{1/(n+2)}\zeta_0\,, \quad\quad\quad \zeta_0 = \left[\frac{(n+2)^{1+n}2^{1-n}}{n\pi^{n/2}}\right]^{1/(n+2)} \left[\frac{\Gamma(1/2 + 1/n)}{\Gamma(1/n)}\right]^{n/(n+2)}\,, \]](form_408.png)
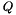is the integral over the whole space, and 
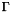is the gamma function.
The setup is built to compare the numerical solution with the analytical one.
.
Configurations (EXPLICIT and STS):
References:
Definition in file init.c.
| void Init | ( | double * | us, |
| double | x1, | ||
| double | x2, | ||
| double | x3 | ||
| ) |
The Init() function can be used to assign initial conditions as as a function of spatial position.
| [out] | v | a pointer to a vector of primitive variables |
| [in] | x1 | coordinate point in the 1st dimension |
| [in] | x2 | coordinate point in the 2nd dimension |
| [in] | x3 | coordinate point in the 3rdt dimension |
The meaning of x1, x2 and x3 depends on the geometry:
![\[ \begin{array}{cccl} x_1 & x_2 & x_3 & \mathrm{Geometry} \\ \noalign{\medskip} \hline x & y & z & \mathrm{Cartesian} \\ \noalign{\medskip} R & z & - & \mathrm{cylindrical} \\ \noalign{\medskip} R & \phi & z & \mathrm{polar} \\ \noalign{\medskip} r & \theta & \phi & \mathrm{spherical} \end{array} \]](form_173.png)
Variable names are accessed by means of an index v[nv], where nv = RHO is density, nv = PRS is pressure, nv = (VX1, VX2, VX3) are the three components of velocity, and so forth.
Definition at line 54 of file init.c.
Assign user-defined boundary conditions.
| [in,out] | d | pointer to the PLUTO data structure containing cell-centered primitive quantities (d->Vc) and staggered magnetic fields (d->Vs, when used) to be filled. |
| [in] | box | pointer to a RBox structure containing the lower and upper indices of the ghost zone-centers/nodes or edges at which data values should be assigned. |
| [in] | side | specifies the boundary side where ghost zones need to be filled. It can assume the following pre-definite values: X1_BEG, X1_END, X2_BEG, X2_END, X3_BEG, X3_END. The special value side == 0 is used to control a region inside the computational domain. |
| [in] | grid | pointer to an array of Grid structures. |
Assign user-defined boundary conditions in the lower boundary ghost zones. The profile is top-hat:
![\[ V_{ij} = \left\{\begin{array}{ll} V_{\rm jet} & \quad\mathrm{for}\quad r_i < 1 \\ \noalign{\medskip} \mathrm{Reflect}(V) & \quad\mathrm{otherwise} \end{array}\right. \]](form_235.png)
where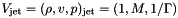 
and M is the flow Mach number (the unit velocity is the jet sound speed, so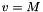 
).
Assign user-defined boundary conditions:
x < 1/6 and reflective boundary otherwise.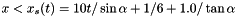
we use fixed (post-shock) values. Unperturbed values otherwise.Assign user-defined boundary conditions at inner and outer radial boundaries. Reflective conditions are applied except for the azimuthal velocity which is fixed.
Assign user-defined boundary conditions.
| [in/out] | d pointer to the PLUTO data structure containing cell-centered primitive quantities (d->Vc) and staggered magnetic fields (d->Vs, when used) to be filled. | |
| [in] | box | pointer to a RBox structure containing the lower and upper indices of the ghost zone-centers/nodes or edges at which data values should be assigned. |
| [in] | side | specifies on which side boundary conditions need to be assigned. side can assume the following pre-definite values: X1_BEG, X1_END, X2_BEG, X2_END, X3_BEG, X3_END. The special value side == 0 is used to control a region inside the computational domain. |
| [in] | grid | pointer to an array of Grid structures. |
Set the injection boundary condition at the lower z-boundary (X2-beg must be set to userdef in pluto.ini). For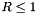 
we set constant input values (given by the GetJetValues() function while for $ R > 1 $ the solution has equatorial symmetry with respect to the z=0 plane. To avoid numerical problems with a "top-hat" discontinuous jump, we smoothly merge the inlet and reflected value using a profile function Profile().
Provide inner radial boundary condition in polar geometry. Zero gradient is prescribed on density, pressure and magnetic field. For the velocity, zero gradient is imposed on v/r (v = vr, vphi).
The user-defined boundary is used to impose stress-free boundary and purely vertical magnetic field at the top and bottom boundaries, as done in Bodo et al. (2012). In addition, constant temperature and hydrostatic balance are imposed. For instance, at the bottom boundary, one has:
![\[ \left\{\begin{array}{lcl} \DS \frac{dp}{dz} &=& \rho g_z \\ \noalign{\medskip} p &=& \rho c_s^2 \end{array}\right. \qquad\Longrightarrow\qquad \frac{p_{k+1}-p_k}{\Delta z} = \frac{p_{k} + p_{k+1}}{2c_s^2}g_z \]](form_395.png)
where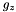 
is the value of gravity at the lower boundary. Solving for 
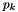at the bottom boundary where 
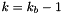gives:
![\[ \left\{\begin{array}{lcl} p_k &=& \DS p_{k+1} \frac{1-a}{1+a} \\ \noalign{\medskip} \rho_k &=& \DS \frac{p_k}{c_s^2} \end{array}\right. \qquad\mathrm{where}\qquad a = \frac{\Delta z g_z}{2c_s^2} > 0 \]](form_399.png)
where, for simplicity, we keep constant temperature in the ghost zones rather than at the boundary interface (this seems to give a more stable behavior and avoids negative densities). A similar treatment holds at the top boundary.
Definition at line 147 of file init.c.
1.8.10