PLUTO
Macros | Functions
math_ode.c File Reference

Ordinary differential equation solvers. More...

#include "pluto.h"
Include dependency graph for math_ode.c:

Go to the source code of this file.

Macros

#define ODE_NVAR_MAX   256
 

Functions

static int RK4Solve (double *, int, double, double, void(*rhs)(double, double *, double *))
 
static int CK45Solve (double *, int, double, double *, void(*rhs)(double, double *, double *), double)
 
void ODE_Solve (double *y0, int nvar, double xbeg, double xend, double dx, void(*rhs)(double, double *, double *), int method)
 

Detailed Description

Ordinary differential equation solvers.

Author
A. Mignone (migno.nosp@m.ne@p.nosp@m.h.uni.nosp@m.to.i.nosp@m.t)
Date
June 20, 2014

Definition in file math_ode.c.

Macro Definition Documentation

#define ODE_NVAR_MAX   256

Definition at line 16 of file math_ode.c.

Function Documentation

int CK45Solve ( double *  y0,
int  nvar,
double  x0,
double *  dx0,
void(*)(double, double *, double *)  rhs,
double  tol 
)
static

Definition at line 140 of file math_ode.c.

147 {
148  int i, n, rhs_err, isgn, useZ=0;
149 
150  double scrh, err, dx_shrink, dx_grow;
151  double Yscal, dx;
152 
153  const double a2 = 0.2;
154  const double a3 = 0.3;
155  const double a4 = 0.6;
156  const double a5 = 1.0;
157  const double a6 = 0.875;
158 
159  const double c1 = 37.0/378.0;
160  const double c2 = 0.0;
161  const double c3 = 250.0/621.0;
162  const double c4 = 125.0/594.0;
163  const double c5 = 0.0;
164  const double c6 = 512.0/1771.0;
165 
166  const double cs1 = 2825.0/27648.0;
167  const double cs2 = 0.0;
168  const double cs3 = 18575.0/48384.0;
169  const double cs4 = 13525.0/55296.0;
170  const double cs5 = 277.0/14336.0;
171  const double cs6 = 0.25;
172 
173  const double b21 = 0.2;
174  const double b31 = 3.0/40.0 , b32 = 9.0/40.0;
175  const double b41 = 0.3 , b42 = -0.9, b43 = 1.2;
176  const double b51 = -11.0/54.0, b52 = 2.5, b53 = -70.0/27.0, b54 = 35.0/27.0;
177  const double b61 = 1631.0/55296.0, b62 = 175.0/512.0, b63 = 575.0/13824.0, b64 = 44275.0/110592.0, b65 = 253.0/4096.0;
178 
179  double y1[ODE_NVAR_MAX], ys[ODE_NVAR_MAX];
180  double y4th[ODE_NVAR_MAX], y5th[ODE_NVAR_MAX];
181  double k1[ODE_NVAR_MAX], k2[ODE_NVAR_MAX], k3[ODE_NVAR_MAX];
182  double k4[ODE_NVAR_MAX], k5[ODE_NVAR_MAX], k6[ODE_NVAR_MAX];
183 
184  dx = (*dx0);
185 
186 /* -- check increment sign -- */
187 
188  if (dx < 0.0) isgn = -1;
189  else isgn = 1;
190 
191 /* -- make a safety copy of the initial condition -- */
192 
193  for (n = 0; n < nvar; n++) y1[n] = y0[n];
194 
195 
196  rhs (x0, y0, k1);
197  for (n = 0; n < nvar; n++) ys[n] = y1[n] + dx*b21*k1[n];
198 
199  rhs (x0 + a2*dx, ys, k2);
200  for (n = 0; n < nvar; n++) ys[n] = y1[n] + dx*(b31*k1[n] + b32*k2[n]);
201 
202  rhs (x0 + a3*dx, ys, k3);
203  for (n = 0; n < nvar; n++) {
204  ys[n] = y1[n] + dx*(b41*k1[n] + b42*k2[n] + b43*k3[n]);
205  }
206 
207  rhs (x0 + a4*dx, ys, k4);
208  for (n = 0; n < nvar; n++) {
209  ys[n] = y1[n] + dx*(b51*k1[n] + b52*k2[n] + b53*k3[n] + b54*k4[n]);
210  }
211 
212  rhs (x0 + a5*dx, ys, k5);
213  for (n = 0; n < nvar; n++) {
214  ys[n] = y1[n] + dx*(b61*k1[n] + b62*k2[n] + b63*k3[n]
215  + b64*k4[n] + b65*k5[n]);
216  }
217 
218  rhs (x0 + a6*dx, ys, k6);
219 
220 /* -- compute 5th and 4th order solutions -- */
221 
222  for (n = 0; n < nvar; n++) {
223  y5th[n] = y1[n] + dx*(c1*k1[n] + c2*k2[n] + c3*k3[n]
224  + c4*k4[n] + c5*k5[n] + c6*k6[n]);
225  y4th[n] = y1[n] + dx*(cs1*k1[n] + cs2*k2[n] + cs3*k3[n]
226  + cs4*k4[n] + cs5*k5[n] + cs6*k6[n]);
227  }
228 
229 /* --------------------------------------------------------
230  compute error
231 
232  the following should give an absolute error if the
233  solution is close to zero and a relative one in the
234  limit of large |Y|
235  -------------------------------------------------------- */
236 
237  err = 0.0;
238  for (n = 0; n < nvar; n++) {
239  scrh = fabs(y5th[n] - y4th[n])/(1.0 + fabs(y1[n]));
240  err = MAX(err, scrh);
241  }
242 
243  err /= tol;
244 
245  if (err < 1.0){ /* -- ok, accept step -- */
246 
247  err = MAX(err, 1.e-18);
248 
249  /* -- provide an estimate for next dx -- */
250 
251  dx_grow = 0.9*fabs(dx)*pow(err, -0.2);
252  dx_grow = MIN(dx_grow, 5.0*fabs(dx)); /* -- do not increase more than 5 -- */
253  *dx0 = isgn*dx_grow;
254 
255  for (n = 0; n < nvar; n++) y0[n] = y1[n] = y5th[n];
256  return 0;
257 
258  }else{ /* -- shrink dx and redo time step -- */
259 
260  dx_shrink = 0.9*fabs(dx)*pow(err, -0.25);
261  dx = MAX(dx_shrink, 0.05*fabs(dx)); /* -- do not decrease more than 20 -- */
262  *dx0 = isgn*dx;
263  return 1;
264  }
265 }
MAX
#define MAX(a, b)
Definition: macros.h:101
n
static int n
Definition: analysis.c:3
configure.scrh
tuple scrh
Definition: configure.py:200
MIN
#define MIN(a, b)
Definition: macros.h:104
ODE_NVAR_MAX
#define ODE_NVAR_MAX
Definition: math_ode.c:16
i
int i
Definition: analysis.c:2

Here is the caller graph for this function:

void ODE_Solve ( double *  y0,
int  nvar,
double  xbeg,
double  xend,
double  dx,
void(*)(double, double *, double *)  rhs,
int  method 
)

Main driver for the numerical integration of a system of standard ordinary differential equations (ODEs) of the type

\[ \frac{dy}{dx} = f(x,y) \]

where x is the independent variable and y[] is a vector of unknowns.

Parameters
[in,out]y0on input, y0 is an array containing the initial condition at x=xbeg; on output it is replaced by the value of the function at x=xend
[in]nvaran integer number specifying the number of variable (i.e. the dimension of y0[])
[in]xbegthe initial integration point
[in]xendthe final integration point
[in]dxthe initial (suggested) step size
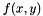[in]rhsa pointer to a function of the form rhs(x,*y,*f) giving the right hand side $f(x,y)$ of the ODE.
[in]methodan integer specifying the integration algorithm. Possible choices are ODE_RK4 (fixed step size, 4th order Runge-Kutta), ODE_CK45 (adaptive step size, 5th order Cash-Karp algorithm).

Definition at line 23 of file math_ode.c.

49 {
50  int nv, i, nsteps;
51  double x0, x1;
52 
53  nsteps = (int)((xend - xbeg)/dx);
54 
55  x0 = xbeg;
56 
57 /*printf ("[ODE_Solve] xbeg = %12.6e, xend = %12.6e\n",xbeg, xend); */
58 
59  while (x0 < xend){
60 
61  /* -- shorten step size to match final integration point -- */
62 
63  if (method == ODE_RK4){
64 
65  RK4Solve(y0, nvar, x0, dx, rhs);
66  x0 += dx;
67 
68  }else if (method == ODE_CK45){
69  int err, k=0;
70  double dx0;
71 
72  dx0 = dx; /* -- save initial step size -- */
73 
74  while (++k) {
75  if ((x0+dx) > xend) {
76  dx = xend - x0;
77  }
78  x1 = x0 + dx;
79  err = CK45Solve (y0, nvar, x0, &dx, rhs, 1.e-9);
80  if (err == 0) {
81  x0 = x1;
82  break;
83  }
84  if (fabs(dx/dx0) < 1.e-4) {
85  print ("! ODE_Solve: step size too small \n");
86  QUIT_PLUTO(1);
87  }
88  if (k > 16384){
89  print ("! ODE_Solve: too many steps\n");
90  print ("! xbeg = %f, xend = %f\n",xbeg, xend);
91  QUIT_PLUTO(1);
92  }
93  }
94 
95  }else{
96  print1 ("! ODE_Solve: integration method unknown\n");
97  QUIT_PLUTO(1);
98  }
99  }
100 }
ODE_CK45
#define ODE_CK45
Definition: math_tools.h:28
print1
void print1(const char *fmt,...)
Definition: amrPluto.cpp:511
ODE_RK4
#define ODE_RK4
Definition: math_tools.h:27
RK4Solve
static int RK4Solve(double *, int, double, double, void(*rhs)(double, double *, double *))
Definition: math_ode.c:103
k
int k
Definition: analysis.c:2
print
void print(const char *fmt,...)
Definition: amrPluto.cpp:497
CK45Solve
static int CK45Solve(double *, int, double, double *, void(*rhs)(double, double *, double *), double)
Definition: math_ode.c:140
i
int i
Definition: analysis.c:2
QUIT_PLUTO
#define QUIT_PLUTO(e_code)
Definition: macros.h:125

Here is the call graph for this function:

int RK4Solve ( double *  y0,
int  nvar,
double  x0,
double  dx,
void(*)(double, double *, double *)  rhs 
)
static

Definition at line 103 of file math_ode.c.

109 {
110  int nv;
111  double y1[ODE_NVAR_MAX];
112  double k1[ODE_NVAR_MAX], k2[ODE_NVAR_MAX];
113  double k3[ODE_NVAR_MAX], k4[ODE_NVAR_MAX];
114 
115 /* -- step 1 -- */
116 
117  rhs (x0, y0, k1);
118  for (nv = 0; nv < nvar; nv++) y1[nv] = y0[nv] + 0.5*dx*k1[nv];
119 
120 /* -- step 2 -- */
121 
122  rhs (x0 + 0.5*dx, y1, k2);
123  for (nv = 0; nv < nvar; nv++) y1[nv] = y0[nv] + 0.5*dx*k2[nv];
124 
125 /* -- step 3 -- */
126 
127  rhs (x0 + 0.5*dx, y1, k3);
128  for (nv = 0; nv < nvar; nv++) y1[nv] = y0[nv] + dx*k3[nv];
129 
130 /* -- step 4 -- */
131 
132  rhs (x0 + dx, y1, k4);
133  for (nv = 0; nv < nvar; nv++)
134  y0[nv] += dx*(k1[nv] + 2.0*(k2[nv] + k3[nv]) + k4[nv])/6.0;
135 
136  return (0);
137 }
ODE_NVAR_MAX
#define ODE_NVAR_MAX
Definition: math_ode.c:16

Here is the caller graph for this function: