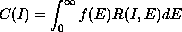
Although we use a spectrometer to try to find out the spectrum of a source, what the spectrometer obtains is not the actual spectrum, but rather a spectrum consisting of photon counts (C) within specific instrument channels, (I). This observed spectrum is related to the actual spectrum of the source (f(E)), such that:
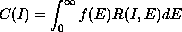
where R(I,E) is the instrumental response and is a measure of the probability that an incoming photon of energy E will be detected in channel I. Ideally, then, we would like to determine the actual spectrum of a source (f(E)) by inverting this equation, thus deriving f(E) for a given set of C(I). Regrettably, this is not possible in general, as such inversions tend to be non-unique and unstable to small changes in C(I). (For examples of attempts to circumvent these problems see Blissett & Cruise 1979; Kahn & Blissett 1980; Loredo & Epstein 1989).
The usual alternative is to try to choose a model spectrum (f(E))
that can be described in terms of a few parameters (i.e., f(E,p1,p2,...)),
and match, or ``fit" it to the data obtained by the spectrometer. For
each f(E), a predicted count spectrum (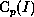
) is calculated and
compared to the observed data (C(I)). A ``fit statistic'' then is
computed from the comparison, which enables one to judge whether the
model spectrum ``fits'' the data obtained by the spectrometer.
The model parameters then are varied to find the parameter values that
give the most desirable fit statistic. These values are referred to
as the best-fit parameters. The model spectrum (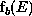
) made
up of the best-fit parameters is considered to be the best-fit model.
The most common fit statistic in use for determining the ``best-fit"
model is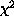 
, defined as follows:
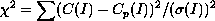
where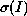 
is the error for channel I (e.g., if C(I) are counts
then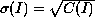 
).
Once a ``best-fit" model is obtained, one must ask two questions:
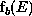(and not some other model). The answer to this
question is known as the ``goodness-of-fit" of the model.
The 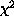statistic provides a well-known goodness-of-fit criterion
for a given number of degrees of freedom (
, which is calculated
as the number of channels minus the number of model parameters) and
for a given confidence level. If 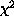exceeds a critical value
(tabulated in many statistics texts) one can conclude that 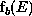is
not an adequate model for C(I). As a general rule, one wants
the ``reduced 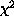" (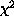/) to be approximately
equal to one (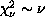
). A reduced 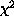that is much
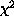greater than one indicates a poor fit, while a that is much
less than one indicates that the errors on the data have been over-estimated.
Even if the best-fit model (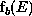) does pass the ``goodness-of-fit" test, one still
cannot say that 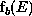is the only acceptable model. For example, if the data used in the
fit are not particularly good, one may be able to find many different models for which adequate
fits can be found. In such a case, the choice of the correct model to fit is a matter of scientific
judgement.
The confidence interval for a given parameter is computed by varying the
parameter value until the 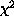increases by a particular amount above the
minimum, or ``best-fit" value.
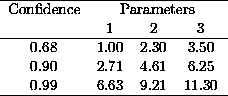
The amount that the 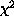is allowed to increase (also referred to as the critical
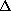
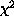) depends on the confidence level one requires, and on the
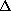
number of parameters whose confidence space is being calculated. The critical for
common cases are given in the following table
(from Avni, 1976):
There is a good discussion of confidence ranges in Press et al., (1992)
for readers who want more details
.